Philippe Moireau's habilitation defense
Philippe Moireau is defending his research habilitation today in Amphi Sophie Germain. Please download his manuscript here.
Research News
Mathematical and numerical modelling of coaxial cables
Derivation and justification of a generalised telegraphist’s model for coaxial cables In this work, we focus on the time-domain simulation of the propagation of electromagnetic waves in non-homogeneous lossy coaxial cables. The full 3D Maxwell equations, that described the propagation of current and electric potential in such cables, are classically Continue ReadingMathematical and numerical modelling of coaxial cables
Wave-based inverse problems
Transient elastography The approach studied here is to be linked to the so-called hybrid inverse problems. Having been made available internally as the solution of a preliminary wave based inverse problem, the full-field measurements considered are used to construct by local algebraic manipulations a system, possibly redundant, of PDE whose Continue ReadingWave-based inverse problems
Efficient time discretization for wave equations
High order theta schemes for the wave equation High order theta schemes are new time discretisation schemes for the wave equation based upon the modified equation technique and the implicit theta scheme. In the context of a (high order) finite element discretization in space of a wave equation the following Continue ReadingEfficient time discretization for wave equations
Mathematical and Numerical Modelling of piezoelectric sensor
Justification of an approximate 3D model for piezoelectric sensors Piezoelectric sensors are widely used for ultrasonic non destructive testing as they can convert an elastodynamic wave into a difference of potential and vice versa, they are used both as emitter and receiver. The behavior of such devices is governed by Continue ReadingMathematical and Numerical Modelling of piezoelectric sensor
Perfectly matched layers for wave equations
Perfectly matched layers for the water wave equation The water wave equations model gravity wave generation and propagation in water, in its complete form, it read as solving a homogeneous Laplacian problem in water coupled with a non linear boundary condition on the surface, depending on time. A simpler Continue ReadingPerfectly matched layers for wave equations
Application of cardiac modeling to optimize pacemaker strategies in Cardiac Resynchronisation Therapy
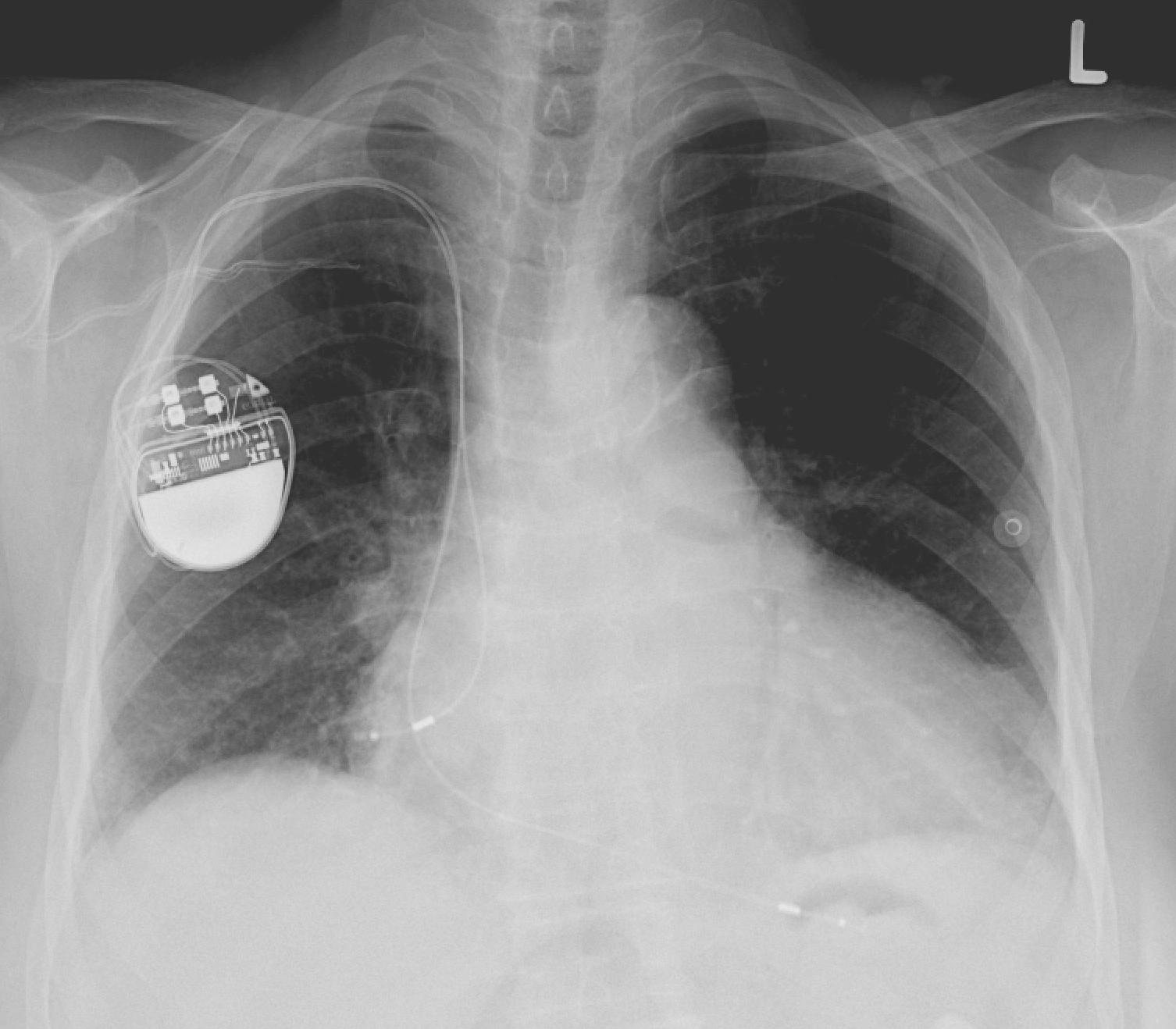
Cardiac resynchronisation therapy (CRT) is an effective treatment for patients with congestive heart failure and a wide QRS complex. However, up to 30% of patients are non-responders to the pacemaker implant in terms of exercise capacity or left ventricular reverse remodelling. A number of controversies still remain surrounding patient selection, Continue ReadingApplication of cardiac modeling to optimize pacemaker strategies in Cardiac Resynchronisation Therapy
State observers for the wave or elasticity equations in bounded domains
We consider a second-order hyperbolic equation in a bounded domain, for example the wave equation or the elasticity system. On this system we assume that the initial condition is unknown, but that we have at our disposal some measurements in time on the solution. Typically, for the wave equation we Continue ReadingState observers for the wave or elasticity equations in bounded domains
Joint state and parameter sequential estimation for PDEs
Our objective is to address a large class of identification problems for PDEs with original methods coming from observer - also called sequential estimator - methods. In fact, in identification the most widely used method consists in minimizing a least-square functional involving a data discrepancy term and some regularization terms. Continue ReadingJoint state and parameter sequential estimation for PDEs
Data assimilation in fluid-structure interaction - Application to the cardiovascular system
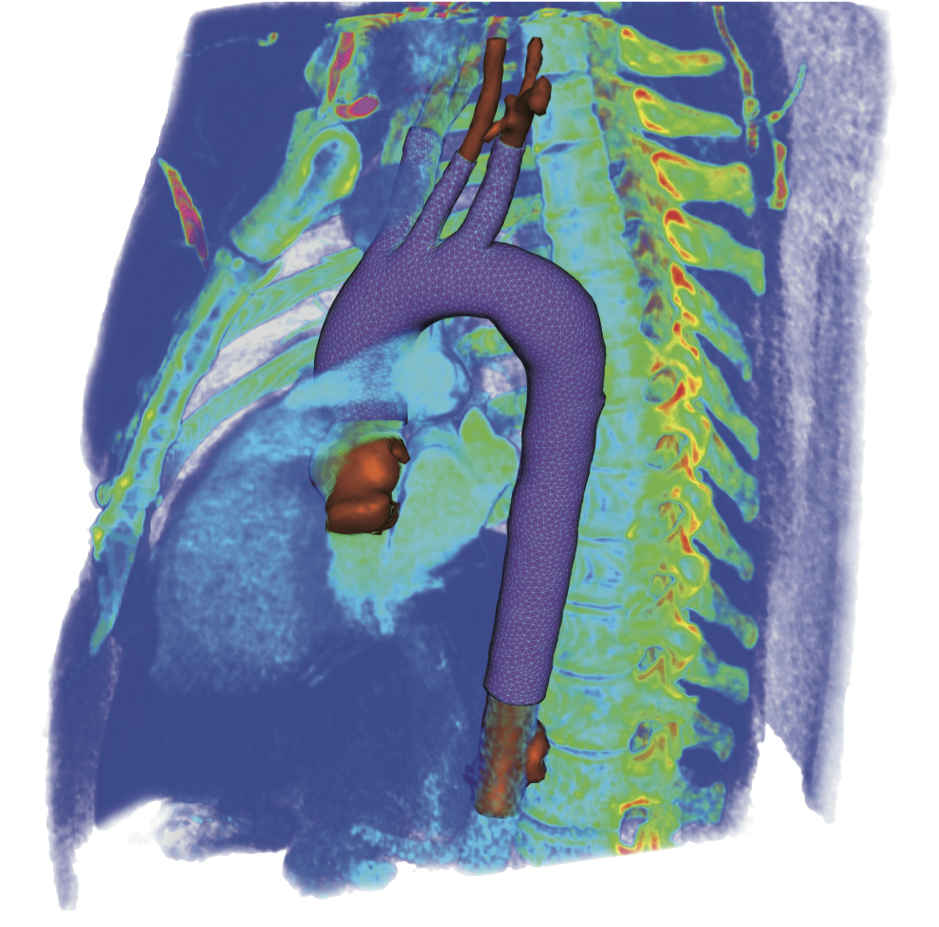
This joint work with Charles Taylor's Lab at Stanford and the Reo team at Inria Paris-Rocquencourt was initiated with the objective of applying data assimilation strategies to produce patient-specific simulations of a section of the arterial tree. We focused on a healthy patient for which the main difficulty was to Continue ReadingData assimilation in fluid-structure interaction - Application to the cardiovascular system