Perfectly matched layers for the water wave equation
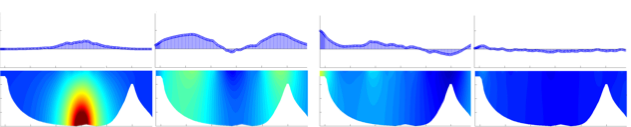
The water wave equations model gravity wave generation and propagation in water, in its complete form, it read as solving a homogeneous Laplacian problem in water coupled with a non linear boundary condition on the surface, depending on time. A simpler model is obtained by linearizing the surface condition in order to only describe the propagation of the gravity wave, which is sufficient for waves of small amplitudes compared to the deepness of the bottom and the wavelength. To take into account the propagation of linearized water waves problem in unbounded domains original absorbing perfectly matched layers (PML) have been developed.
Perfectly matched transmission problem with absorbing layers : application to anisotropic acoustics in convex polygonal domains
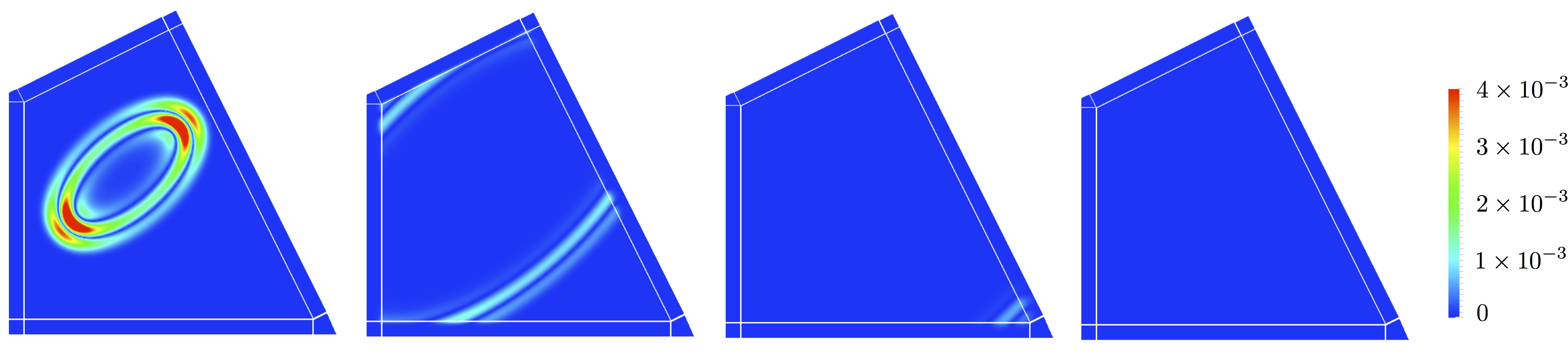
The question of unbounded domains naturally arises in various wave type problems, matched layers enable to simulate the propagation in homogeneous infinite medium. They are non physical layers in which the amplitude of the wave will exponentially decrease. They are perfectly matched when no reflections occurs at the interface between these layers and the physical domain. A formulation adapted to anisotropic acoustics has been developed as well as a numerical scheme based upon high order mortar elements to deal with transmission conditions.
