High order theta schemes for the wave equation
High order theta schemes are new time discretisation schemes for the wave equation based upon the modified equation technique and the implicit theta scheme. In the context of a (high order) finite element discretization in space of a wave equation the following semi-discrete equation is obtained:
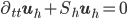
The most classical time discretization is the explicit second order leap frog scheme (1). Modified equation technique allows to achieve higher order time discretizations, as illustrated by the fourth order scheme (2).
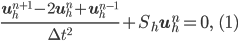
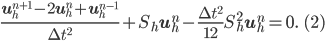
It can be shown, using energy techniques, that these schemes are stable under a condition on the time step that depends on the mesh. In general, explicit discretization is a very efficient approach, but when strong mesh refinement is needed (for instance in presence of singular geometries), this can lead to a very severe time step restriction. To avoid this locking effect, it is possible to use the standard second order theta-scheme (3). This scheme is implicit and unconditionally stable for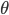 
greater than 1/4, and the cost of the required matrix inversion is compensated by the fact that the time step can be arbitrarily large. However, the use of large time step induces a loss of precision.
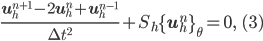
where
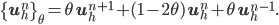
We propose a family of schemes of the form (4) based on the modified equation technique, which extend the theta-scheme to higher order time discretizations:
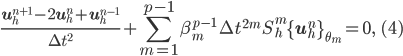
where the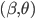 
are chosen coefficients such that the scheme is stable and minimises the consistency error.