(Closed) PhD position on Shape observers for elastodynamics problems – Applications to medical imaging and to the characterisation of red blood cells

In mechanics, can we physically characterize a dynamical system by observing its shape variations? More precisely, given an (infinite-dimensional) dynamical system, how can we assimilate the shape of the deforming domain to estimate the complete solution and eventually identify some physical parameters?

Our problem belongs to the category of data assimilation problems, as a type of inverse problem formulation where the system of interest is a dynamical system, and the data at our disposal are collected through time. Historically, data assimilation has appeared in the 70's in the context of geophysics, but has now also reached new fields of research, e.g. in life sciences. The question of the profound nature of the available data has always been of great concern, especially when working with image data such as satellite images in weather forecasting, or in medical imaging in life sciences, where we perceive only a "shadow" of the system behavior. For many years, the general workflow was to perform complex data processing on these images in order to be able to compare, in the chosen data assimilation procedure, the model to natural outputs that it could have directly generated. This is, however, at the cost of uncontrolled regularization and errors introduced in the data processing. More recently, some works have already set out to consider the data as they are. Nevertheless, in most cases, the methods are formal or applied after space and time discretization, which limits their analysis. Oftentimes, they are also based on model simplifications to make them more directly compatible with the data, but at the cost of modeling consistency errors.

Our objective is to avoid over-simplified models or over-processed data. Let us consider a system class typically defined by a partial differential equation (PDE) system, and abstractly represented as a dynamical system of the form

$\dot{y} = A(y(t),\theta,\nu(t)), t > 0; \quad (y(0), \theta, \nu) \text{ unknown, }$

where $y$ is the state variable in an adequate functional space with --~possibly --~an uncertain initial condition $y(0)$ , $\theta$ is a set of unknown parameters in some regular space (possibly finite dimensional) and $\nu$ some additional model noise in a functional space to be defined (potentially stochastic). Here we consider a mechanical system whose deformation is governed by the elastodynamics equations defined on a reference domain $\Omega(0)$ . For this system, we have at our disposal some observations on a target state variable $\breve{y}$ represented by an image $\mathcal{I}[\breve{y}]$ which gives the shape of the domain $\Omega(t)$ deforming over time. In order to formulate a data assimilation strategy based on these measurements, we need an adequate discrepancy between the measurements $\Omega(t)$ and the corresponding domain $\hat{\Omega}(t)$ simulated in time. We propose a similarity measure inspired by the Mumford-Shah theory in image analysis [Morel 1995,Vese 2002,Collin 2015]

(1) $\begin{equation*} \begin{cases} \displaystyle \mathscr{D}: (y,\mathcal{I}) \mapsto \int_{\Omega(t)} \hspace{-0.3cm} \bigl|\mathcal{I}[\breve{y}](x,t) - C_1(t)\bigr|^2 dx + \int_{\Omega^c(t)} \hspace{-0.3cm} \bigl|\mathcal{I}[\breve{y}](x,t) - C_2(t)\bigr|^2 dx, \\ \hspace{2cm} \text{with } \displaystyle C_1(t) = \frac{1}{|\Omega(t)|} \int_{\Omega(t)} \hspace{-0.3cm} \mathcal{I}[\breve{y}](\xi,t) d\xi,\quad C_2(t) = \frac{1}{|\Omega^c(t)|} \int_{\Omega^c(t)} \hspace{-0.3cm} \mathcal{I}[\breve{y}](\xi,t) d\xi. \end{cases} \end{equation*}$

One possible strategy would be to rely on an optimization procedure where we minimize $\int_0^T \mathscr{D} dt$ under the constraint of the system dynamics \eqref{eq:system}. This strategy, inspired from optimal control, is known as the variational approach in data assimilation. A more original point of view --~and sometimes more effective --~consists in adopting a so-called observer strategy where we define a joint observer $(\hat{y}\;\; \hat{\theta})^\intercal$ that pursues the target trajectory and parameters via a feedback control $B = (B_y \; B_\theta)^\intercal$ only depending of the similarity measurement, hence leading to

(2) $\begin{equation*} \begin{cases} \dot{\hat{y}} = A(\hat{y},\hat{\theta},0) + B_y(\mathcal{I},\nabla \mathscr{D}), t > 0; \quad \hat{y}(0) = y_0 \text{ \emph{a priori} knowledge} \\ \dot{\hat{\theta}} = B_\theta(\mathcal{I},\nabla \mathscr{D}), t > 0; \quad \hat{\theta}(0) = \theta_0 \text{ \emph{a priori} knowledge} \end{cases} \end{equation*}$

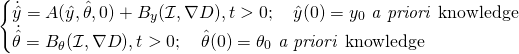
This observer approach has also shown great promises in elastodynamics with our pioneer work on the subject [Moireau 2009,Imperiale 2013]. However, extending our approach to the Mumford-Shah functional is challenging as this similarity term is not a standard least square data fitting term. We typically envision 6 research directions:

Formulate the adequate shape similarity measures adapted to the system of interest, and design the control feedback $B_y$ ;
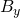Prove the existence of the observer system \eqref{eq:observer} solution;
Obtain stabilization properties demonstrating how the simulated system can be controlled to the target trajectory;
Extend the state observer ( 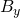$B_y$ alone) to a joint state-parameter observer (with 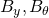$B_y, B_\theta$ ), and analyze of identification properties;
Propose and analyze adequate discretization and numerical strategies;
Apply in a real context with medical imaging and experimental setup.

In practice, this problem is of primary concern in cardiovascular or pulmonary modeling applications. Indeed, if we expect biomechanical models proposed in the literature to be used in a diagnosis or prognosis context, these models must be adapted to the specific condition of each patient. In this respect, the large amount of data collected on the patient is of major help, but non-invasive data are generally images shaping the patient state. For instance, we only image the shape of the myocardium domain deforming during a heartbeat and identically we now image the shape of the deforming lungs to estimate the impact of the breathing on the development of fibrosis tissues [Hinz 2016]. Registering the complete biophysical models of the patient's organs directly via these shape data is a Graal for definitely introducing physical models in medical diagnosis.

MRI sequence and heart segmentations (left,courtesy VP2HF) versus simulations (right)

We also believe that our approach has application in another biomechanical context that includes fluid-structure interaction models. We are starting a collaboration with A.V. Salsac from UTC Compiegne who aims at identifying mechanical properties of deforming capsules -~with applications to red blood cells --~under observation of their shape change in a canal --~representing a capillary [Hu 2013]. In this context, our observer furnishes an original estimator after extending it to the fluid-structure interaction context as we have already done for more classical mechanical observers [Bertoglio 2011]. For this application, M. Fernandez, a specialist in fluid structure formulations and numerical analysis will also be associated.

Example of 2 capsules, flowing down the microchannel (a) Pictures of the deformed capsule shape. (b) Corresponding superposition of the experimental (dotted line) and numerical (continuous line) profiles (right). Courtesy A.V. Salsac [Hu 2013]

Candidate profile
For this subject, we are thus looking for a candidate with a strong level in PDEs, control, numerical analysis with also a multidisciplinary background on mechanics and also biomechanics. Indeed, we in particular expect the candidate to be strongly motivated by a close collaboration with biomechanicians and experimentalists of UTC Compiègne for the study of the deforming capsules.

Bibliography

[Bertoglio 2011] C. Bertoglio, D. Chapelle, M.A. Fernández, J-F. Gerbeau, and P. Moireau. State observers of a vascular fluid-structure interaction model through measurements in the solid. Comput. Meth. Appl. Mech. Engrg, 256(2013) :149–168, 2011.
[Collin 2015] A. Collin, D. Chapelle, and P. Moireau. A Luenberger observer for reaction-diffusion models with front position data. ournal of Computational Physics, 300(1) :288–307, 2015.
[Hinz 2016] B. Hinz and B. Suki. Does Breathing Amplify Fibrosis ? Am. J. Respir. Crit. Care Med., 194(1) :9–11, July 2016.
[Hu 2013] X. Q. Hu, B. Sévénié, A. V. Salsac, E. Leclerc, and D. Barthès-Biesel. Characterizing the membrane properties of capsules flowing in a square-section microfluidic channel : Effects of the membrane constitutive law. Phys Rev E, 87(6) :063008–9, 2013.
[Imperiale 2013] A. Imperiale, A. Routier, S. Durrleman, and P. Moireau. Improving Efficiency of Data Assimilation Procedure for a Biomechanical Heart Model by Representing Surfaces as Currents. In FIMH, 2013.
[Moireau 2009] P. Moireau, D. Chapelle, and P. LeTallec. Filtering for distributed mechanical sys- tems using position measurements : perspectives in medical imaging. Inverse Problems, 25(3) :035010, 2009.
[Morel 1995] J.M. Morel and S. Solimini. Variational Methods in Image Segmentation. Birkhauser Boston Inc., 1995.
[Vese 2002] L.A. Vese and F.C. Chan. A multiphase level set framework for image segmentation using the Mumford and Shah model. International Journal of Computer Vision, 50(3) :271–293, 2002.